Logarithms can seem tricky at first, but once you understand how they work, they're really useful for solving exponential equations. From population growth to pH levels and sound intensity, they have a variety of real-world applications. Here, we'll explore what they are, the rules that govern them, and how you can apply them.
What Are Logarithms?
A logarithm is basically the inverse of an exponent. Exponents tell us how many times to multiply a number by itself; logarithms are the answer to the question "What power do I raise the base to to get this number?"
In mathematical terms:
Here:
is the base, a positive number not equal to 1,
is the value (sometimes called the argument),
is the exponent or power.
For example:
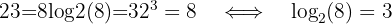
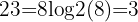
This means the logarithm 
equals 3 because 2 raised to the power of 3 gives 8.
You’ll often meet these kinds of problems in exams where you’re asked to solve tricky questions
involving exponents and logarithms. Most students will encounter logs in their algebra or higher-level maths courses. For those studying science, engineering, and finance, they'll likely encounter logs when algebraic techniques are not applicable because the unknown is in the exponent.
Why Learn Logarithms in Maths?
Students will likely wonder why they should spend their time learning about logarithms. Logs are more than an abstract maths idea, though; they can be used in science, technology, and everyday life. Logs also come up in maths and physics when studying motion and forces. Logarithms are used to explain growth or decay at an exponential rate. Examples include:
- Population growth can be described using exponential functions, and logs help us work backwards to calculate time or growth rates.
- In chemistry, the pH scale is logarithmic, measuring the concentration of hydrogen ions.
- Engineers use logarithms in decibels to describe sound intensity.
- Economists apply logs to study compound interest and inflation.
Logs are the only method by which you can solve equations when the unknown is in the exponent.
Before calculators and computers, mathematicians and scientists depended on log tables to simplify their work. These tables list the logarithmic values of many numbers, allowing people to replace complex multiplication and division with easier addition and subtraction using the rules of logs. For centuries, log tables were an essential tool in navigation, astronomy, and engineering, saving hours of manual calculation and reducing costly errors.
Understanding Logarithmic Notation
The general form of a logarithm is:
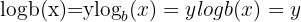
This tells us that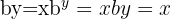 
, where:
- is the base (a positive number, not equal to 1),
- is the argument (the result we’re taking the log of),
- is the exponent.
In practice, two special types appear most often in maths:
- Common logarithm:
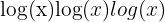, which uses base 10. - Natural logarithm:
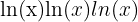, which uses base 
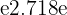approx 
.
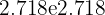Common Types of Logarithms (Base 10 and Natural Log)
Not all logarithms use the same base. You'll typically encounter two special types:
Common Logarithm (Base 10):
Written as 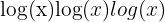without showing the base. This is often used in science and engineering because our number system is decimal. For example:
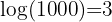
since
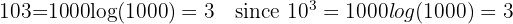
since
Natural Logarithm (Base 
):
Written as
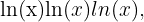
where
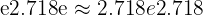
This constant is as important in mathematics as π\piπ. The natural logarithm appears in growth and decay formulas, calculus, and probability theory. For example:
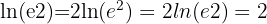
Technically, you can define a logarithm with any positive base except 1. However, these two examples are so common that calculators have dedicated buttons for them. That said, the change of base formula allows you to work with logs of any base.
Exponentials and Their Inverses
Logarithmic functions “undo” exponentials. For example, if an exponential equation looks like:
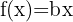
then the corresponding logarithmic function is its inverse:
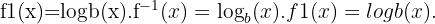
This inverse relationship means that applying an exponent and then a log (or vice versa) brings you back to the original number:
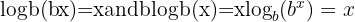
and
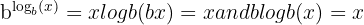
This property makes logs powerful in solving equations. For example, consider:
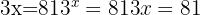
Since
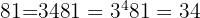
we know immediately that:
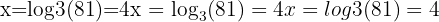
When the right-hand side is not a neat power, logarithms allow us to isolate the exponent, making them a valuable function in algebra and calculus. If you’re moving into calculus, logs become even more important since they’re directly tied to derivatives and integrals, which are used in differentiation/integration problems.
The Core Log Rules Every Student Must Know
There are three core log rules. These include the product, quotient, and power rules. With these, you can simplify expressions and solve equations. Let's explore them.
1. Product Rule
The logarithm of a product is equal to the sum of the logarithms:
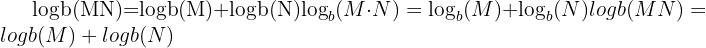
Example:
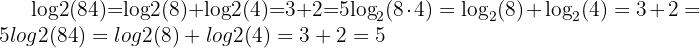
This rule is handy when breaking down large numbers or combining terms in algebraic equations.
2. Quotient Rule
The logarithm of a quotient is equal to the difference of the logarithms:
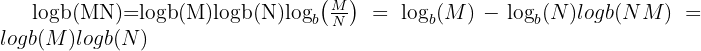
Example:
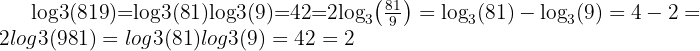
This is particularly handy when simplifying fractions inside logarithmic expressions.
3. Power Rule
An exponent inside a log can be brought out in front as a multiplier:
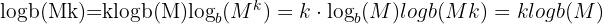
Example:
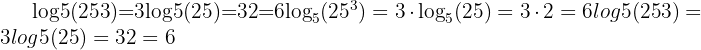
This rule makes it much easier to handle variables in exponents, since you can rewrite them as coefficients. These three properties form the backbone of algebraic work with logs, and they reappear frequently in Calculus and higher-level maths courses.
Additional Rules of Logs and Properties
After you've gained some confidence with the three core laws, there are other logarithm rules you can use to work with complex expressions.
Log of 1
Any logarithm with an argument of 1 equals 0:
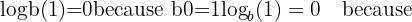
because
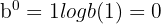
because
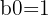
Example:
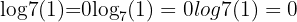
Log of the Base
The logarithm of a base to itself is always 1:
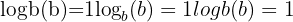
Example:
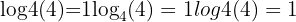
Change of Base Formula
Calculators usually only support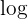 
(base 10) and 
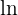(base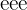 
). To work with other bases, you use the change of base rule:
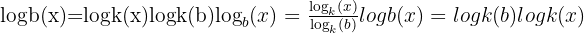
Most often:
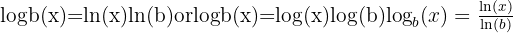
or
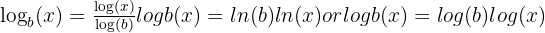
Example:
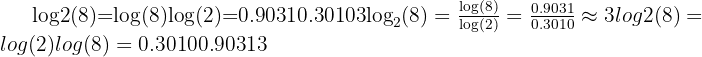
Restrictions: Zero and Negative Arguments
Logarithmic functions are only defined for positive numbers:
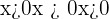
That means:
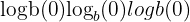has no real solution.
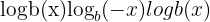is undefined unless you are working with complex numbers.
Whenever you’re solving equations, always check that your solution doesn’t make the log undefined.
Students often make the same errors when first working with logarithms. One of the most common is trying to take the logarithm of zero or a negative number, which has no real solution. Another mistake is attempting to apply log rules when the bases are different, which only works if you first use the change of base formula. A final issue arises with extraneous solutions: when solving equations, always check that the solution does not make the argument of a log invalid. Remembering these points will prevent unnecessary mistakes in both practice and exams.
Solving Logarithmic Equations Step by Step
Once you're familiar with the rules of logs, start applying them to solve equations. Any equation that contains a log expression is a logarithmic expression, and you'll usually have to isolate the variable.
1. Equations with a Single Log
If the equation contains just one logarithm, you can rewrite it in exponential form.
Example:
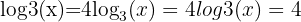
Step 1: Convert to exponential form:
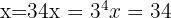
Step 2: Simplify:
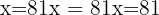
2. Equations with Logs on Both Sides
When both sides of the equation have logarithms (with the same base), you can “drop” the logs and solve the resulting algebraic equation.
Example:
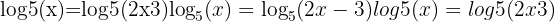
Step 1: Remove the logs:
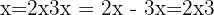
Step 2: Solve:
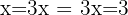
3. Equations That Require Log Rules
Sometimes, you need to combine logs using the product, quotient, or power rule before converting.
Example:
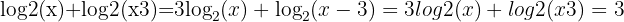
Step 1: Apply the product rule:
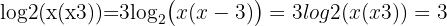
Step 2: Convert to exponential form:
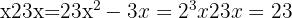
Step 3: Simplify:
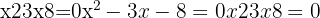
Step 4: Solve the quadratic:
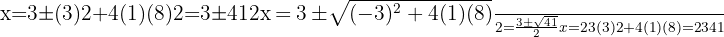
Remember: solutions must make the log’s argument positive.
to high precision.
Practice Examples and Activities
Time to practice using the main log rules. Here are some worked examples for you to have a go yourself.
Example 1: Product Rule
Simplify:
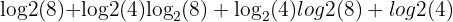
Solution:
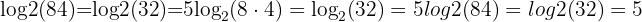
Try it yourself:
Example 2: Quotient Rule
Simplify:
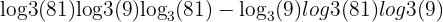
Solution:
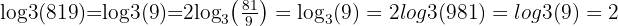
Try it yourself:
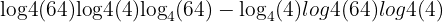
Example 3: Power Rule
Simplify:
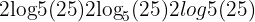
Solution:
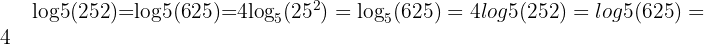
Try it yourself:
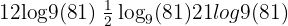
Example 4: Mixed Log Expression
Simplify:
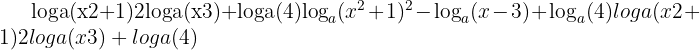
Solution:
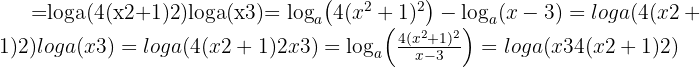
Try it yourself:
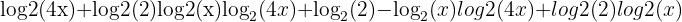
Example 5: Exponential Equation
Solve:
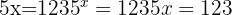
Solution:
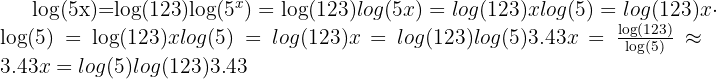
Try it yourself:
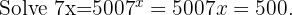
The most effective way to become confident with logarithms is through regular practice. Past exam papers, online worksheets, and guided exercises give you the chance to apply log rules in many contexts. When you are solving, write down every stage of your working, even if you are not sure of the final answer, as examiners often award marks for correct methods. If you find yourself stuck, break the problem down into smaller steps and apply one log rule at a time. Always check your solutions with a calculator or by sketching a quick graph to confirm the result.
Enjoyed this article? Leave a rating!
Loading...
